Fitting a line to data in linear regression

Link: Linear regresssion

Residual sum of squares/sum of squared residuals §

The distance from a line to a data point is called *residual.

Residual sum of squares (RSS)* are the differences between the data and the line. We sum the square of these values, because the square result won’t neglect the positive/negative value.

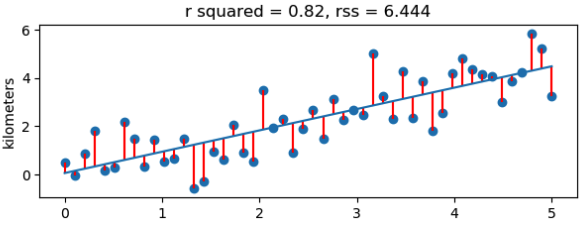
The more fit it gets, the RSS is smaller.

Notation §

$$\begin{gathered} \text{SS (sum of squares)}={\text{(data - mean)}}^2 \\ \text{variation around the mean}=\frac{{\text{(data - mean)}}^2}{n} \\ \text{var(mean)}=\frac{\text{SS(mean)}}{n} \end{gathered}$$

In this way, var() can be viewed as the average SS.

Least squares §

Least squares is the method to find the best values for a and b in the linear regression model $y=ax+b$. The name, obviously, comes from “the least of RSS”.

1. The concept is to minimize the square of the distance between the observed value and the line.
2. This can be achieved by taking the derivative and finding where it’s equal to 0 (by computer).

Note that there’s another similar method called Weighted least squares which we can use in Fitting a curve to data.