Logistic regression

Link: Supervised learning

Logistic regression §

What is logistic regression? §

• Logistic regression is a method for classification
• It helps classification: either 0 or 1
• It’s a specific type of generalized linear model(GLM)

Why to use logistic regression, and not liner regression §

1. Because normal linear regression model on binary groups
   1. Result is either 0 or 1, while linear regression is a continuous line which can go beyond 0 or 1 (beyond limit)
   2. It poorly fits the data
2. Logistic regression is a transformed form of linear regression

Sigmoid Function/Logistic Function §

What is Sigmoid Function (Logistic function) ? §

A function to transform any value to be between 0 and 1

$$\varphi (z)=\frac{1}{1+e^{-z}}$$

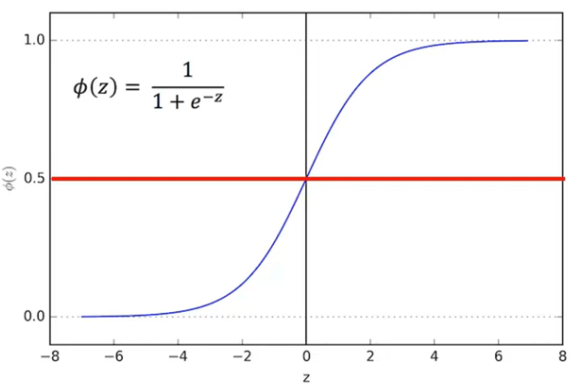
How to use it in evaluation? §

We can set cutoff point at 0.5:

1. Below 0.5 belongs to 0
2. Above 0.5 belongs to 1

How to interpret when the point is in 0.5? §

There’s a 50/50 chance that the result is either 0 or 1.

Explain the math: where does it comes from? §

Linear regression model:

$$y=b_0+b_{1}x$$

Transformed to Logistic regression model:

$$p=\frac{1}{1+e^{-(b_0+b_{1}x)}}$$

Evaluate the model §

Using Confusion matrix

Simple example of confusion matrix §

A simple example to predict disease:

n=165	Predicted: N	Predicted: Y
Actual: N	50 (TN)	10 (FP=Type-I)	60
Actual: Y	5 (FN=Type-II)	100 (TP)	105
	55	110

Terminology §

• True Positives (TP)
• True Negatives (TN)
• False Positives (FP): Type-I error
• False Negatives (FN): Type-II error

Evaluate with confusion matrix §

Accuracy rate §

$$Accuracy=\frac{TP+TN}{total}$$

In the example:

$$Accuracy=\frac{TP+TN}{total}=\frac{100+50}{165}=0.91$$

Misclassification rate (Error rate) §

$$Error=\frac{FP+FN}{total}$$

In the example:

$$Error=\frac{FP+FN}{total}=\frac{10+5}{165}=0.09$$