Link: Statistical test
Hypothesiss testing
Below chart illustrate the recover time of drug A and drug B. What hypothesis we could draw from below chart?
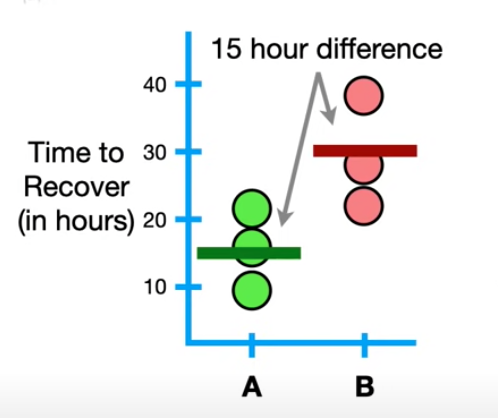
People taking drug A need 15 more hours on average to recover than who taking drug B.
However, if we repeat the experiment many times and get opposite result, we can confidently reject this hypothesis.
If we have data that is similar to the hypothesis but not exactly the same, then we say it’s fail to reject the hypothesis.
Null hypothesis
The hypothesis that there is no difference between things is called Null hypothesis.
With null hypothesis, we don’t need lots of preliminary data to make such statement because details are not needed in this hypothesis.
Example of default and balance: meaning p of default is not related to the variable balance.
In this case:
- Z-value > 2, meaning it statistically significant from 0, so rejects
- P-value < 0.05, confirmed its significanty (used as evidence to reject )
Abstract
Null hypothesis can be anything, it’s just a term to describe an outcome. It’s usually related to “whether it happened/not happened” because it’s easier to calculate the p-value for testing hypothesis.
Null hypothesis and alternative hypothesis
Null hypothesis and Alternative hypotheses are paired. It can be think of they are two different distribution, and our goal is to pick the best distribution from the two.
No matter whether it’s linear/logistic/normal distribution, we can think of this way. In null hypothesis, the parameter is 0, representing one kind of distribution. While it’s equal to others, it represents other forms of distribution.