Power analysis

Link: Statistical power Population and estimated parameters

Instead of P-hacking by adding more data points after the result, we can do Power analysis to determine the sample size of experiements.

What is Power analysis? §

A power analysis determines what the sample size should be to ensure we have a good amount of Statistical power.

Two main factors of power §

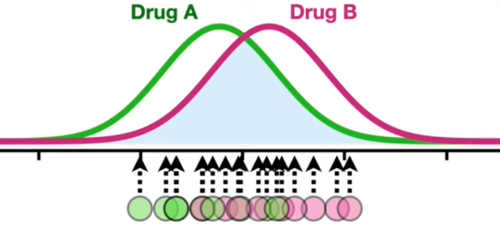
1. How much overlap between the two distributions
2. The sample size (the number of measurements)

Example: when there’re lots of overlap, we need more measurements in order to correctly reject the null hypothesis.

Why the power analysis would work §

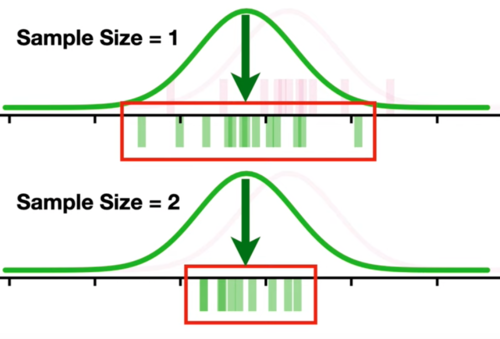
Sample 1: 1 measurement = 1 estimated mean Sample 2: 2 measurements = 1 estimated mean (the avg of two)

The intuition of power analysis §

If we only pick 1 measurement, it may come from the tails of distribution (but we don’t know) which can easily disrupt the total sample.

However, if we pick 2 measurements and get the average as the estimates, the chances that both come from tails are pretty low. Therefore, we can get a more accurate result. AKA, extreme measurements have less effect on the estimates.

How to do power analysis §

Decide how much power we want §

Common threshold: 0.8

Determine the threshold for significance §

The significance is often called $\alpha$, usually 0.05

Estimate the overlap between distributions §

The overlap is determined by:

1. The distance between distributions
2. Standard deviation

Effective size is a created formula to reflect the overlap.

$$\text{Effect size}(d)=\frac{\text{Estimated difference in means}}{\text{Pooled estimated sd}}$$

One of the simplest way to get pooled estimated standard deviation is:

$$\text{Pooled estimated sd}=\sqrt{\frac{s_1^2+s_2^2}{2}}$$

Google “statistics power calculator” §

Input:

1. Power = ?
2. Threshold of significance $\alpha$ = ?
3. Effective size = ?

Output: sample size = ?