Linear regression

Link: Supervised learning

The main idea of linear regression §

1. Use Least squares to Fitting a line to data in linear regression
2. Calculated R-squared
3. Calcualte a P-value for $R^2$

Terminology §

SS(mean) sum of squares around the mean §

$$\text{SS(mean)}={\text{(data - mean)}}^2$$

Var(mean) variation around the mean §

$$\text{var(mean)}=\frac{{\text{(data - mean)}}^2}{n}=\frac{\text{SS(mean)}}{n}$$

In this way, var() can be viewed as the average SS.

SS(fit) sum of squares of around the least-squares fit §

$$\text{SS(fit)}={\text{(data - line)}}^2$$

Var(fit) variation around the line §

$$\text{var(fit)}=\frac{\text{SS(fit)}}{n}$$

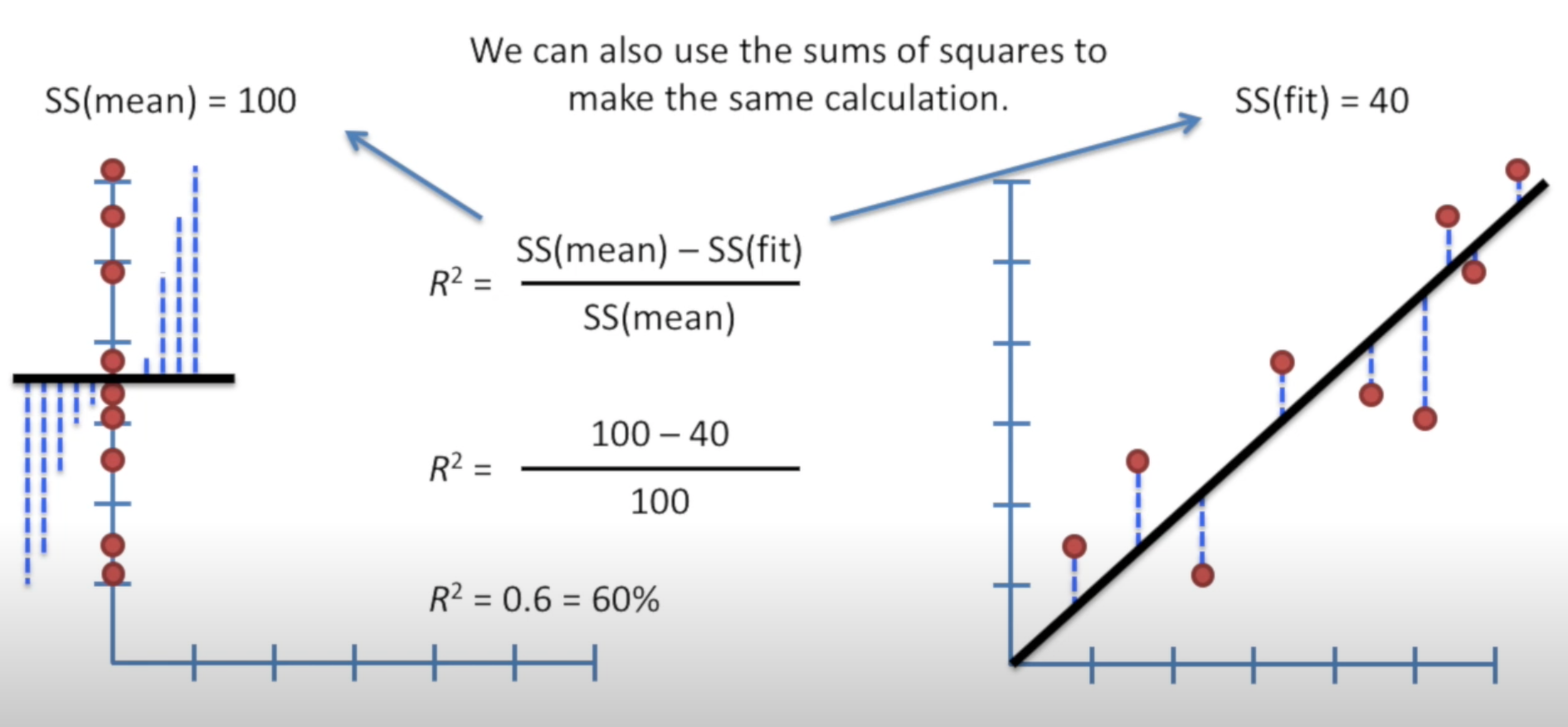
How does it work §

1. Meausre $SS(\text{mean})$

2. Measure $SS(\text{fit})$

3. Plug in and we get $R^2$

   $$R^2=\frac{SS(\text{mean})-SS(\text{fit})}{SS(\text{mean})}$$

   Note that when $SS(\text{fit})$ is 0, then $R^2$ = 1

4. Use p-value to determine if $R^2$ is statistically significant When there’re only two data points for the line, $SS(\text{fit})$ = 0. So we need a p-value to identify things like this. P-value for $R^2$ comes from $F$, the F-value.

F-value §

$$F=\frac{\text{the variation in x explained by y}}{\text{the variation in x not explained by y}}=\frac{SS(\text{mean})-SS(\text{fit})/(P_{\text{fit}}-P_{\text{mean}})}{SS(\text{fit})/(n-P_{\text{fit}})}$$

The larger F-value is, it indicates y can explain more variation in x.

$(P_{\text{fit}}-P_{\text{mean}})/(n-P_{\text{fit}})$ is also known as degree of freedom.

Steps to covert F-value to p-value: §

1. Generate a set of random data

2. Calculate the mean and ss(mean)

3. Plug-in and get $F$ value, plot the value in histogram

4. Repeat many times for random datasets

5. Do the same for the original dataset, and get $F_0$. p-value = the number of more extreme values than $F_0$ divided by all F values

F-distributions §

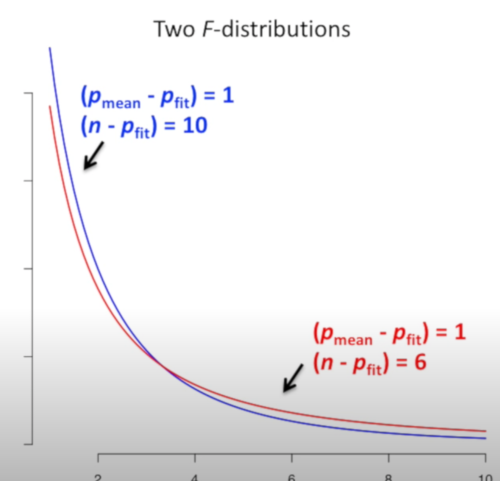
In above example, the sample of red is smaller than blue while other parameters are the same. The blue line is steeper, and thus, when we calculate the probability of the extreme values for getting p-value, the p-value would be smaller. Therefore, more sample size leads to a smaller p-value.