Link: Logistic regression coefficients Hypothesis testing and the null hypothesis
What is p-value?
The p value, or probability value, tells you how likely it is that your data could have occurred under the null hypothesis. It’s between 0 and 1.
- Threshold: 0.05
- Can be used to confirm the Z-value
- e.g. When z < 2, and if p > 0.05, it also confirm it’s not statistically significant
The intuition
If p = 0.05, it means only 5% of the time we would see the null hypothesis, thus, we should reject the null hypothesis.
In short:
- p > 0.05: failed to reject the null hypothesis / reject the alternative hypothesis
- p < 0.05: reject the null hypotheses
Purpose
The p-value tell us how often we would expect to see the extreme statistic. It can help us eliminate some noises (e.g. if the coin is fair, if the drug result has other factors).
Adjust the p-value
A small p-value when there’s no difference is also called False Positive. See P-hacking and false positives for more details. We can adjust the p-value to a smaller threshold, if checking the difference is important to avoid false positive. We can also make the threshold larger, e.g. 0.2 means we are willing to get a False Positive 2 times out of 10 experiements.
The limit of p-value
P-value does not reflect the effect size, aka how different they are. It only tells us whether it’s different.
Two-sided vs One-sided p-value
Usually the *two-sided p-value*(or two-tailed p-value) are mostly common. See details in One-sided p-value(one-tailed p-value).
When to use which p-value?
Example: Testing the effectiveness of a drugs comparing to current treatment
One-sided p-value is 0.03, while two-sided p-value is 0.06.
Which p-value shoud we use?
The one-sided p-value tests the hypothesis that the drug is better than the current. The two-sided p-value tests if the new drug is better/worse/not significantly different than the current one. The former is smaller because it doesn’t cover other scenarios.
Therefore, we should use two-sided p-value because we want to find out whether the drug is better or worse. Based on the similar logic, we usually use two-sided p-value whenever we can.
Note: from statistical best practice, we should always decide what test and which p-value to use before doing the experiment. Otherwise it would be p-hacking and increase the chance of reporting fake results.
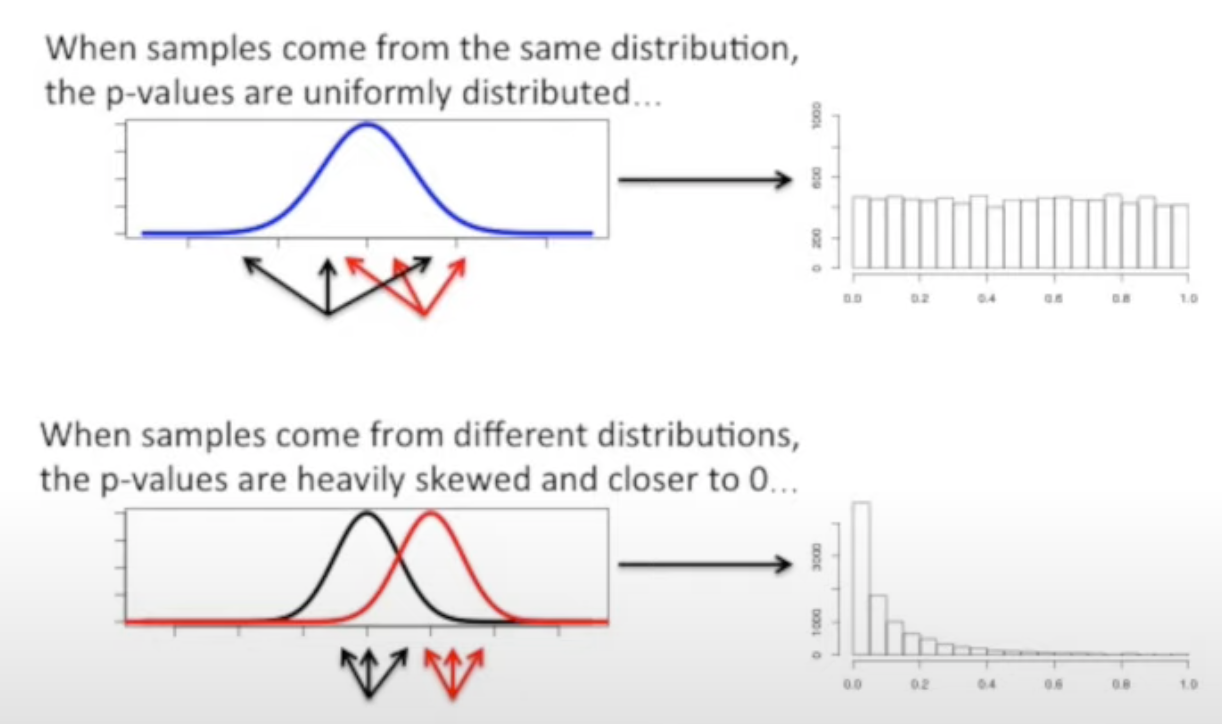
Distribution of p-value
The distribution of p-value is also different when the samples come from the same distribution vs different distributions.